Thermal Noise Floor 174

When drift current dominates the thermal noise is a function of the channel conductance whereas in moderate and weak inversion the diffusion component gives rise to shot noise.

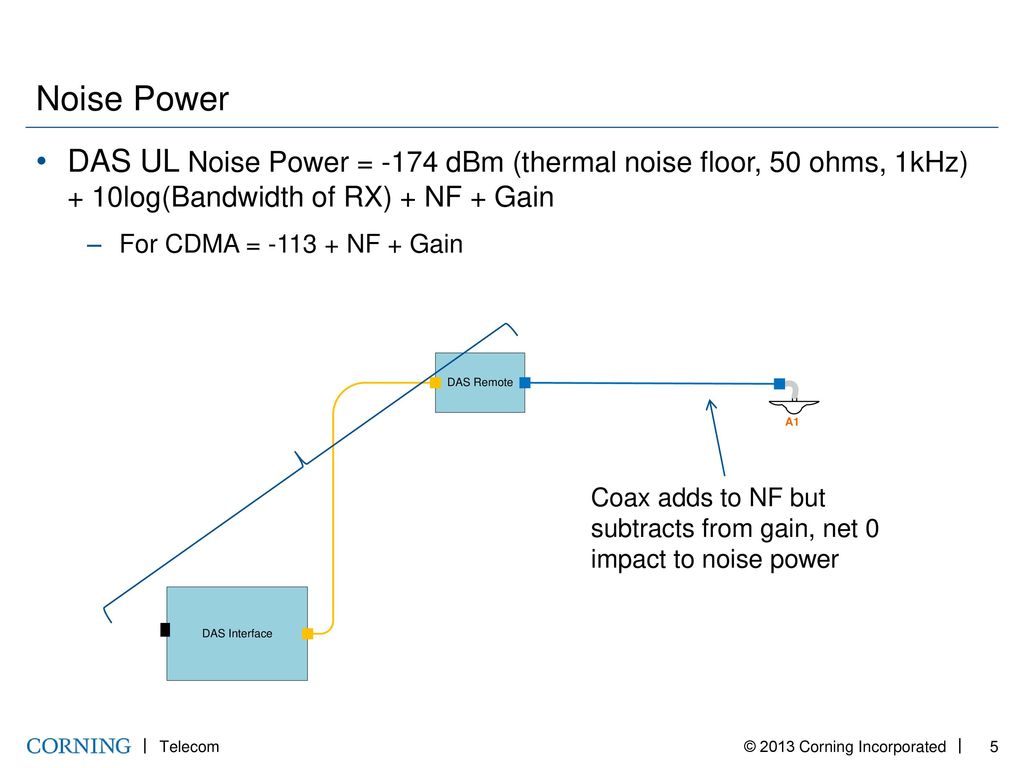
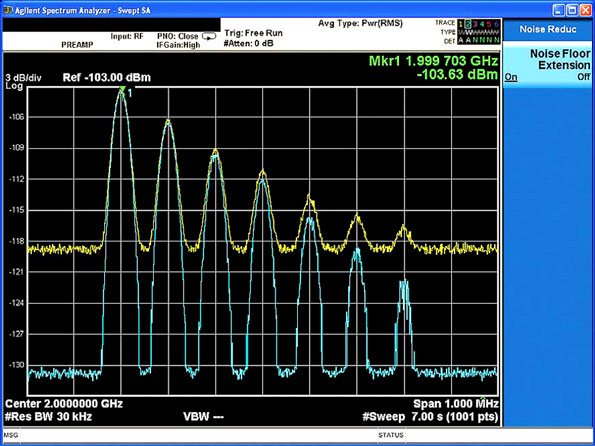
Thermal noise floor 174. It is then easy to relate this to other bandwidths. Thermal noise in a 50 ω system at room temperature is 174 dbm hz. 1 hz noise floor equates to a noise power of 174 dbm so a 1 khz bandwidth would generate 174 10 log 10 1 khz 144dbm of noise power the noise is thermal noise johnson noise. If we look at the normalized b 1 hz bandwidth noise floor equation we have.

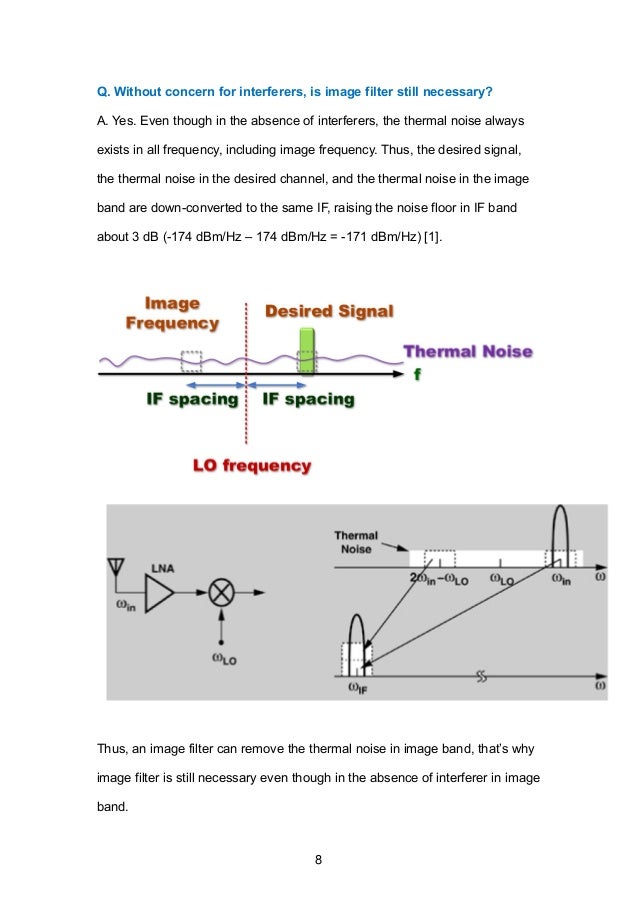
Thermal noise floor k joules k t k b hz the resulting noise is in joules second or watts. Thermal noise is the most widely used but it may also be called johnson nyquist noise johnson noise or nyquist noise. Relative to the bandwidth we can use the reference level of 174 dbm hz and simply multiply it by the actual bandwidth of the radio channel. It is measured in noise power units of dbm or watt or noise voltage.

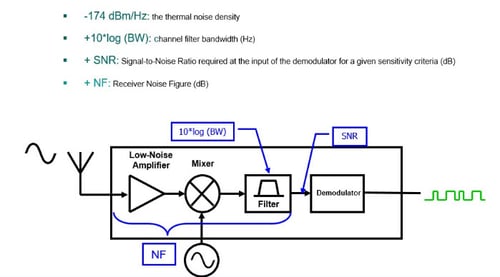
Noisefloor 10 log10 k t b 10 log10 1 38 10 23 290 1 hz. Following equation or formula is used for thermal noise power and voltage calculator. In the absence of any broadband noise sources 1 f noise or brownian noise the minimum noise level you can hope to measure in an electronic system is the thermal noise floor. Noise power of 174 dbm hz is the reference for any noise power calculation when designing rf systems working at room temperature.

Thermal noise spectrum is gaussian in shape. Analyzing noise in general can be difficult as there are a variety of intrinsic noise sources and these intrinsic noise sources are unique to different systems. A good model should capture the drain noise current accurately in all. This noise gained its various names because this noise was first detected and measured by john b.

The noise resulting from thermal agitation of electrons is referred as thermal noise. Let s calculate the thermal noise floor of the 200 khz. Thermal noise power and voltage equation. Thermal noise is relatively well understood in fets and should form the core of any model.

Because the power level is proportional to the bandwidth twice the bandwidth level gives twice the power level 3db and ten times the bandwidth gives ten times the power level 10db. Johnson in 1926 and later explained by harry nyquist both were bell labs and working together.