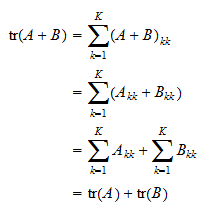Trace Of A Matrix Product

Introduction the trace of a product of matrices has been given extensive study and it is well known that the trace of a product of matrices is invariant under cyclic permutations of the string of matrices 1 p 76.

Trace of a matrix product. The frobenius norm is an extension of the euclidean norm to k n n displaystyle k n times n and comes from the frobenius inner product on the space of all matrices. 4 derivative in a trace 2 5 derivative of product in trace 2 6 derivative of function of a matrix 3 7 derivative of linear transformed input to function 3 8 funky trace derivative 3 9 symmetric matrices and eigenvectors 4 1 notation a few things on notation which may not be very consistent actually. Hence we obtain det a lambda 1lambda 2cdots lambda n note that it is always true that the determinant of a matrix is the product of its eigenvalues regardless diagonalizability. A trivial but often useful property is that a scalar is equal to its trace because a scalar can be thought of as a matrix having a unique diagonal element which in turn is equal to the trace.

Trace of a scalar. In linear algebra the trace of a square matrix a denoted is defined to be the sum of elements on the main diagonal from the upper left to the lower right of a. This property is often used to write dot products as traces. Recall that the trace function returns the sum of diagonal entries of a square matrix.

See the post determinant trace and eigenvalues of a matrix. Puntanen an inequality for the trace of matrix product ieee transactions on automatic control 37 2 239 1992. The trace of a matrix is the sum of its complex eigenvalues and it is invariant with respect to a change of basis this characterization can be used to define the trace of a linear operator in general.